Rotational Kinematics

A rolling object can have 2 motions:

[ Larger ]

 

a) Rotational Motion (radians/s)

b) Translational  Motion - (m/s)

 

Movement of object's center of mass from one (x,y) position to another (x,y) postion

 

 

In order to understand the physics of a rolling object, it's helpful to measure it rotational kinematics in terms of radians.

 

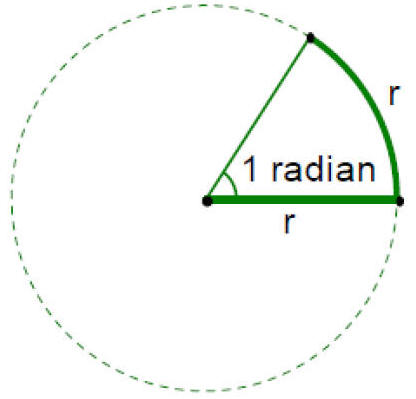
I. Radian

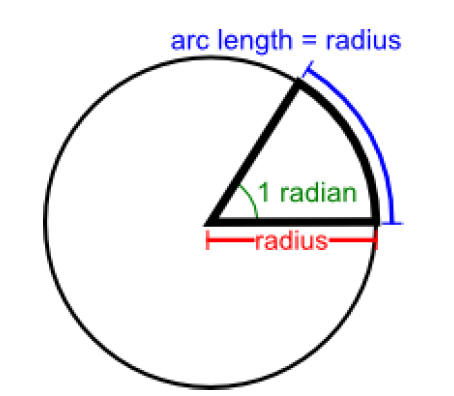
radianPic

 

a) When a round object rotates 1 radian, it has travelled one radii

 

(unit - radian/sec)

 

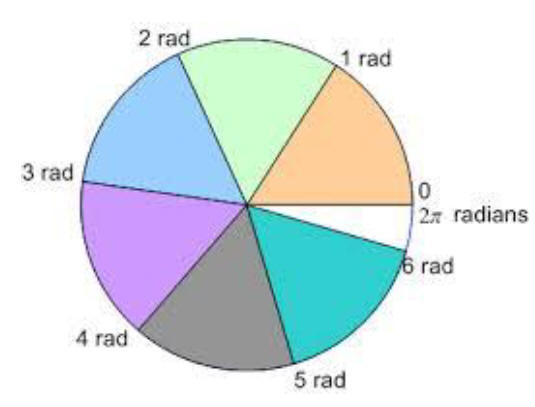
b) One full rotation of a sphere = 360 degrees or .......

[ Larger ]

 

2p radians

 

c) One radian is about ....

 

 

57 degrees

 

d) Converting radians to d

 

Equation:

 

q = d/r

 

And d =

 

d = qr

 

 

 

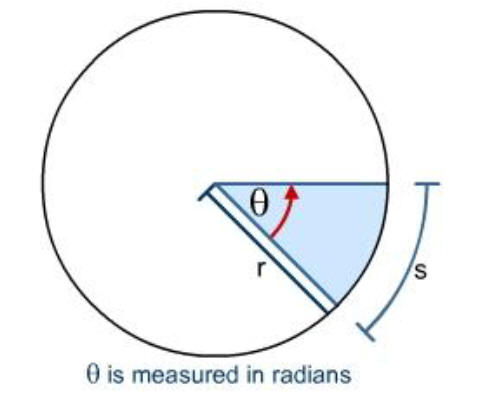
Ex) How many radians does the arc s represent?

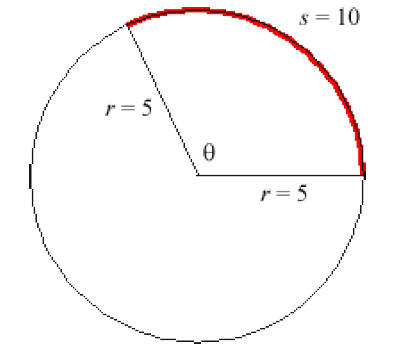
Howmanyradians

Number of radians q =

 

2

 

Ex 1) A wheel with a radius of 2.0 m rolls 5.0 m along the floor.

Find the number of radians rotated through.

 

q = d/r

 

 

2.5 radians

 

 

 

Ex 2) How many radians are subtended by a 0.10 m arc of a circle of radius of 0.40 m?

 

d = qr





.25 radians

Ex 3) How many degrees are subtended by a 0.10 m arc of a circle of radius of 0.40 m?

 

= .25 radians [360°/2pradians]

 

 

14 degrees

 

II. Angular Velocity:

a) defined - How fast something spins

 

b) w = radians/sec

 

c) Linear velocity (v) and Angular velocity w

 

Formula:

 

 v = wr

 

v/r = w

 

 

Ex 4) A ball is rolling along the ground at 5.0 m/s.

If the ball's radius is .50 m, what is its angular velocity?

 

 v = wr

 

5 m/s = w(.50m)

 

w = 10 radians/sec

 

d) Rotating object's period - time
for one complete .....

...  rotation

 

Since w = [2p rad.]/T

 

 

 

T = 2p/w

 

T = 1/f


f = w/2p

 

Ex 5) Find the period for a rolling object with a rotational velocity of 10. rad/sec.

 Find period.

arc

T = 2p/w

 

T = 2p/[10 rad/sec]

 

 

T = .63 sec

 

 

f = 1.6 Hz

 

 

III. Angular Acceleration

 

  • Symbol - a (rad/s2)

Review: Relating Linear motion to Rotational motion

d = rq

q = distance rotated in radians

v = rw

 

w - angular velocity

 

So … a = ra

 

Since a = v2/r

then ..

a = r2w2/r

 

a = rw2

 

Ex 6) A pool ball with a radius of 4.0 cm accelerates from rest to 5.0 m/s in .1 seconds.

 Find its angular acceleration.

Since all the info is linear, find a then convert

 

a = Dw/Dt

 

 

 

a = 50. m/s2 

    
a = ra




a = 1.3 x 103 rad/s2

 

 

 

Match the rotational variable with its linear kinematic variable 

radian3
a =
 
w =

q =
 

 

 

d = ____ v = _____ a = _____

 

Linear Kinematics / Rotational Kinematics Conversion
Linear Kinematics Rotational Kinematics

a = DV/Dt 		 

Vf = Vi + t  		 

V = Dd/Dt 		 

Vf2 = Vf2 + 2aDd 		 

Dd = Vit + ½ at2		  
 

 

Ex 7) A ball with a radius of .10 m starts from rest and accelerates down a 10. m incline and attains a velocity of 8.0 m/s.

Find it’s ANGULAR acceleration.

Find a then a

 

 Vf2 = Vi2 + 2ad

 

 

 

 

 

a = 3.2 m/s2



a = ra


a = 32 rad/s2

 

 

 

 

©Tony Mangiacapre., - All Rights Reserved [Home]
Established 1995
Use any material on this site (w/ attribution)