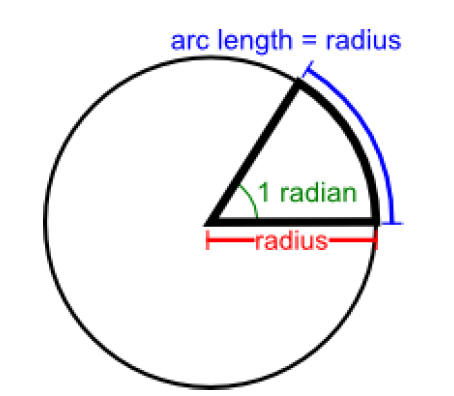
How many radians of rotation produces a 0.10 m arc of a circle of radius 0.40 m?
θ = d / r
θ = 0.10 m / 0.40 m
How many degrees of rotation produces a 0.10 m arc of a circle of radius 0.40 m?
0.25 radians × [ 360° / 2π rad ]
A ball rotates 2π radians in 4.0 s. What is its angular velocity?
ω = 2π radians / 4.0 sec
A toy car rolls in a circular path of radius 0.25 m and the car wheels rotate an arc length of 0.75 m in 8.0 s. What is the angular velocity of the wheels?
v = 0.75 m / 8.0 sec
v = 0.094 m/s
v = ωr → ω = v / r
A mouse is running around in a circle. It starts from rest and accelerates to ω = 12 rad/s in 0.90 s. What is the mouse's angular acceleration?
α = Δω / Δt
A bicycle tire moving at ω = 3.5 rad/s accelerates at a constant rate to 4.2 rad/s in 3.0 s. What is its angular acceleration?
α = Δω / Δt
A bicycle with tires of radius 0.30 m is moving at a constant angular velocity of 2.5 rad/s. What is the linear velocity of the bicycle?
v = ωr
v = (2.5 rad/s)[0.30 m]
A motorbike has tires of radius 0.25 m. If the motorbike is traveling at 4.0 m/s, what is the angular velocity of the tires?
v = ωr → ω = v / r
An elementary school student pushes, with a constant force, a merry-go-round of radius 4.0 m from rest to an angular velocity of 0.80 rad/s in 1.5 s.
a) What is the angular acceleration, α?
α = Δω / Δt
α = 0.80 rad/s / 1.5 sec
b) What is the merry-go-round's tangential acceleration at r = 4.0 m?
a = rα
c) What is the merry-go-round's radial (centripetal) acceleration at 1.5 sec?
a = v² / r
or a = ω²r
d) What is the merry-go-round's total linear acceleration at 1.5 sec?
atotal = √(atangential² + aradial²)
e) What is the frequency of rotation (f) of the merry-go-round at t = 1.5 s?
ω = 2π / T
0.80 rad/s = 2π / T
