Home

Relative Velocity

River with current. Label upstream and downstream

A upstream , B downstream

Ex 1) A boat's speed in still water is 1.85 m/s.

If the boat is to travel directly across a river whose current is 1.20 m/s, at what upstream angle must the boat head?

sinӨ = [1.20 m/s]/[1.85 m/s]

Ө = 40.5° upstream

Crossing a River

When a boat crosses a river,
which component(s) are affected. V_x? V_y?

Only V_x changed
when boat crosses river

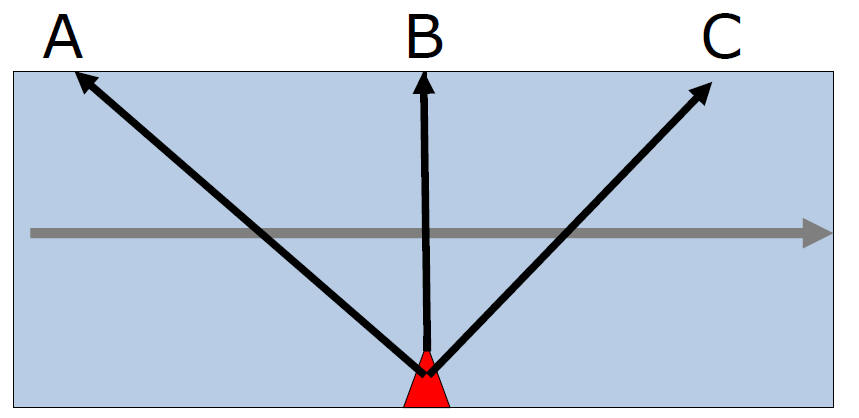
V_r = Velocity of river

V_bx = Boat's x velocity

V_by = Boat's y velocity

Find V_x' 

 Vx' =                                   Vx' =                          Vx'=

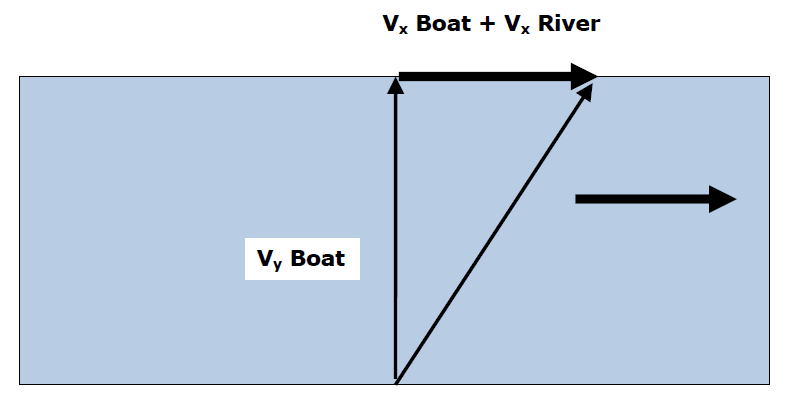
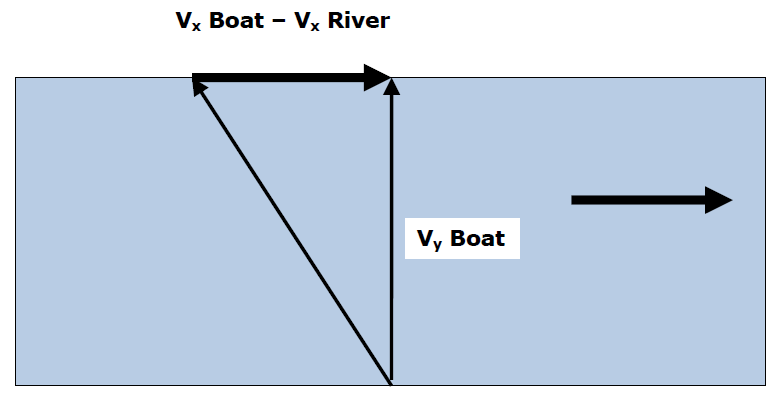
Path B

V_x' = Vr

Path A

V_x' = V_bx - V_r

Path C

V_x' = V_bx + V_r

Downstream
or straight across

V_x increased

Upstream

V_x decreased

V_x' = V_boat +/-  V_river


V_y = V<sub>yboat


V</sub>^'2 = V_x'² + V_y²
 

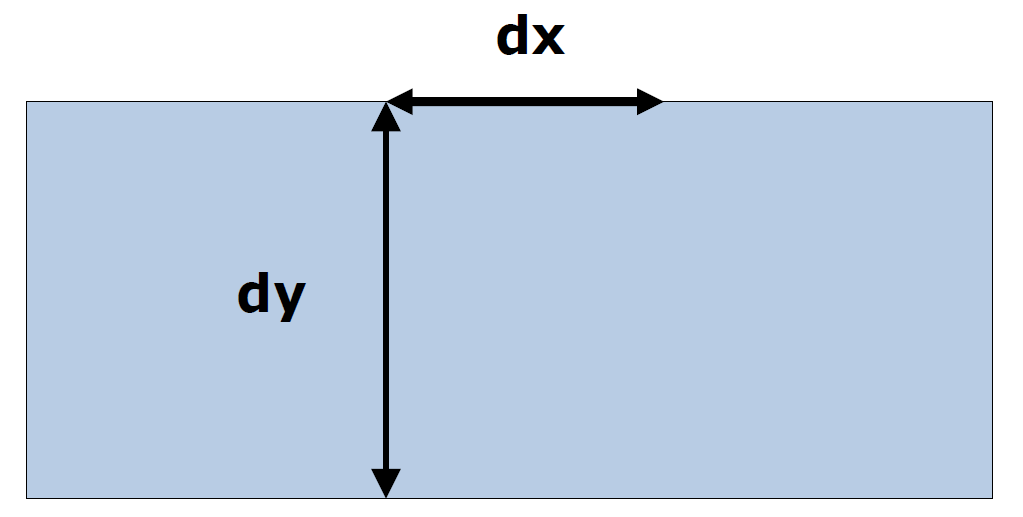
d_x , d_y?

d_y = V_yt

d_x = (V_boat +- V_river)t

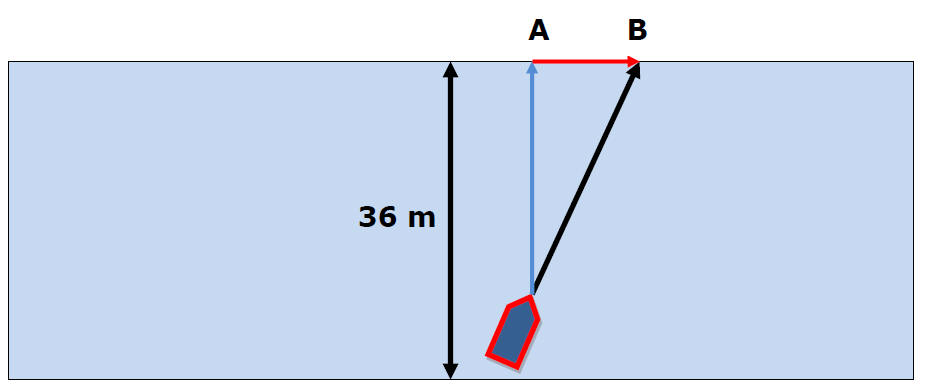
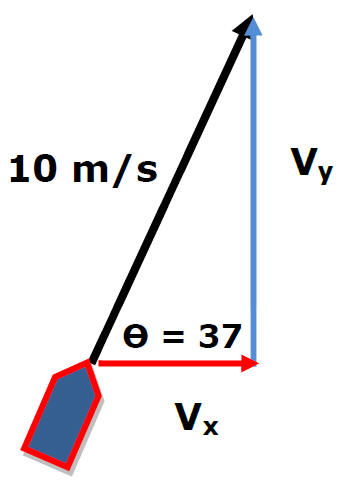
Ex 2) A boat's speed in still water is of 10. m/s. The boat moves downstream across the river at an angle of 37 degrees from the shoreline and reaches opposite shore at point B.

If the velocity of the river is 3.0 m/s, find the time of the trip and distance between A and B. The width of the river is 36 m.

d_x = V_xt

Finding t

d_y = 36m

d_y = V_yt = VsinӨt = 36 m

36 m = 10 m/s[sin37]t

t = 6 sec 

d_x = V_xt

Finding V_x

V_x = V_x boat + V_x river

V_x of Boat

V_x = 10 m/s[cos37] = 8 m/s

V_x River = 3 m/s

V_x = 11 m/s

t = 6 sec 

d_x = V_xt

d_x = 66 m

Intro to
Circular Motion

©Tony Mangiacapre., - All Rights Reserved [Home] Established 1995
Use any material on this site (w/ attribution)